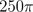Thursday's Class

Today Mr. K went over Quadrilateral Investigation. As Casey said on her scribe post, the properties on the chart : Opposite side are equal, all sides are equal, opposite angle are right angles, consecutive angels are supplementary, diagonals are congruent, diagonals bisect each other, diagonals bisect opposite angles and diagonals are perpendicular to each other.

I hope you don't mind that I'm using your pictures, Casey |D

A parallelogram:

• opposite sides are equal
• consecutive angles are supplementary
• diagonals are congruent
• diagonals bisect each other

A trapezoid:

• opposite angles are right angles

A rectangle:

• opposite sides are equal
• opposite angles are right angles
• consecutive angles are supplementary
• diagonals are congruent
• diagonals bisect each other

A rhombus

• opposite sides are equal
• consecutive angles are supplementary
• diagonals bisect each other
• diagonals bisect opposite angles
• diagonals are perpendicular to each other

A right trapezoid

• consecutive angles are supplementary
  

A square

• opposite side are equal
  
• all sides are equal
• opposite angle are right angles
• consecutive angels are supplementary
• diagonals are congruent
• diagonals bisect each other
• diagonals bisect opposite angles
  
• diagonals are perpendicular to each other

Note that: A square is a special case of a rectangle, as it has four right angles and equal parallel side. It is also a special case of trapezoid, rhombus and parallelogram.

Transversal line is a line that passes through two or more lines at different points.









Later on in the class, Mr. K put us into groups to work on Problem Solving: Geometry 0 & 1 or The Proof is in the Parallelogram. We have to prove that ABRM is a parallelogram

First you have to look at the same sides:

Angle A = Angle R
Angle B = Angle M

Angle A + Angle B + Angle R + Angle M = 360°. That's because Angle A has 90°, angle B has 90°, angle R has 90° and angle M has 90°

2 Angle A + 2 Angle M = 360°. Why ? Because of Angle A = Angle R & Angle M = Angle B.
It's also similar to 2 Angle A + 2 Angle B = 360°
That is why, ABRM is a parallelogram AB // BR and AM // BR


Hopefully, I told you guys everything. I'm really sorry because I'm really bad at explaining stuff, I really tried my best. I'm really sorry that I posted my scribe late. Please, if you didn't understand anything, PLEASE ASK SOMEONE you know that can help you or Mr. K, himself.


MONDAY'S SCRIBE WILL BE .... MARKKKK !!!

November 27, 2008

Today's class, Mr.Kuropatwa put up 2 questions on the board to start off the class.


A. Find the surface area of a prism.







To find the surface area of a prism you have to find the congruent faces. Opposites that have the same area. Find the area of 2 sides (L*w), adjacent sides (w*h), then the two ends (l*w). Then add the total areas. Therefore the answer for the question should be:

SA = 2(2x3) +2 (5x2) +2 (3+5) = 62units²

B. If we triple all the dimensions, what will the new surface area be...Use the pattern we learned yesterday. Although I forgot what the pattern we learned from yesterday, I should of asked again. Answer for the question is:

9x62 = 558

Later on in the class, Mr.K put us into groups to work on a sheet on Quadrilateral. We had to identify figures of shapes with the proper names, examine each figure and identify properties it has in a chart.

The properties on the chart : Opposite side are equal, all sides are equal, opposite angle are right angles, consecutive angles are supplementary. diagonals are congruent, diagonals bisect each other, diagonals bisect opposite angles, diagonals are perpendicular to each other.

The word supplementary means is 2 angles that add up to 180 degrees.
The word congruent means is having the exact equal size and shape.
The word bisect means cutting into 2 congruent in halves.

Mr.K talked a little bit about Convex and Concave but we will be learning more about Convex. He also talked about the Trapezoid being a special quadrilateral ; 2 sides 1 pair parallel (//) *Remember the symbol for parallel* A Parallelogram ; 2 pairs opposite sides parallel. For a rectangle, all sides are congruent. Why? Because all sides are equal to 90 degrees.

Hopefully I covered most of today's scribe. Please bear with me though I'm not good at explaining everything. I tried my best! If you did not understand anything .. PLEASE ask questions in class; it will help you and everyone. :)

TOMORROW'S SCRIBE WILL BE ! ... i-i-i-i-i-i-i-i-i-i.. icon !

November 25, 2008 / Tuesday's Class

Yesterday we started the class of with finding the surface area and volume of each:

a. Sphere









To find the surface area of each sphere, you need to use the formula: 4pr²
(p= pi)

Sphere 1:
4p(1)² = 4p1
4x1xp = 4p

Sphere 2:
4p(2)² = 4p4
4x4xp = 16p

Sphere 3:
4p(3)² = 4p9
4x9xp = 36p

After doing this, you should notice a pattern or a relationship between the spheres above. The end result multiplied by pi have a perfect square in it. By noticing the pattern, you can jump to a sphere that has a radius of 10 instead of doing the formula one after another, after another and so on.
For example, if your trying to find the volume of a sphere that has a radius of 10, I think you have to square the radius and then multiply it by 4, after doing that you multiply it by pi or leave it with the pi sign beside it as your final answer.
*(This is where I personally feel lost, I am not sure how to explain it, hopefully this will help a little. I believe there is more to it, but this is where I am stuck.)*

Now you have to find the volume of each sphere using the formula: 4/3pr³
(p= pi)

Sphere 1:
4/3p(1)³ = 4/3p1
4x1xp divided by 3 = 4p/3

Sphere 2:
4/3p(2)³ = 4/3p8
4x8xp divided by 3 = 32p/3

Sphere 3:
4/2p(3)³ = 4/3p27
4x27xp divided by 3 = 108p/3


b. Cube












Now to find the surface area of each cube you have to use the formula: 6s²

Cube 1:
6x1² = 6x1 = 6

Cube 2:
6x2² = 6x4 = 24

Cube 3:
6x3² = 6x9 = 54

I think there is another pattern, but I am not sure. I have no idea, so I'm just going to leave it as it is.

Now find the volume of each cube using the formula: lwh
Cube 1:
1x1x1 = 1

Cube 2:
2x2x2 = 8

Cube 3
3x3x3 = 27

Since the length, width and the height are all equal, there isn't much to do but to cube the length, width or height.

So most of the class was talking about these questions above and trying to look for a relationship or pattern between them and then we ended the class with sitting in groups trying to figure out these questions below:

1. The area of a shape is 30 cm². If the dimensions of the shape are increased 4 times, what is the area of the new shape?
40 x 4² = 480 cm²

2. The volume of a solid is 24cm³. If the dimensions are tripled, what is the new volume?
24 x 3³ = 648 cm³

Hopefully this scribe helps whoever did not understand the work we did yesterday, I know I got lost in some parts but I didn't say anything.

Today's scribe post will be posted later on tonight by caseyh.

My Muddiest Point

I woke up pretty early today.. my muddiest points:

- word problems that i don't know how to do that involve radicals.
- vocabulary that involve radicals.

before friday:
- simplifying and evaluating, radicals that have a minus sign.

Friday, November 21st, 2008

Today Mr. K first off talked about the blog, telling us how to write label's properly because if you don't, then you won't get the mark's that you deserved for it. Then he moved on mentioning to us that since we were having difficulty with vocabulary, he now will add onto the blog something that will help us out. This is a site found in the right hand side of the blog with a link called "wordequationswiki" sort of like wikipedia, only this time we could add on word's that we don't understand, ourselves to this site.

Our next unit that we began since we had to move on, is called Geometry. For this unit we need to know volume of a cylinder and sphere formula's. There is also another one that we also need to know about, and it is called the baseball theorem. For example, if you take a baseball and cut all the stitches, and then unfold it, it would have 4 circles. And these 4 cirlcles is what is used to find out the surface of a sphere. This is because if you take the 4 circles multiply it by pie and also multiply the radius by itself 2 times, then you would get the surface of a sphere. Note when multiplying with pie you can't just multiply it with just "3.14". You can't just do that you have to use the whole thing because if you were to use "3.14" that'll only be close to pie unlike if you use the whole thing "3.141592654" your answers will be fully correct.

To get us started with Geometry Mr. K gave us an example:

EX) A sphere fits exactly inside a cylinder. Find the volume of each of the size's of cylinder's with spheres inside them. Is there a relationship or a pattern?

First off you have to find the height of the cylinder. You get the height of the cylinder by the diameter of the sphere. And then once that is settled, for all the 3 size's you plug in the measurement's in the formula. For the volume of cylinder formula this is what it would be like : . For the volume of sphere formula it would look like this :

Let's start off with the smaller size first to get you help started and to show you how to do it for the other sizes .

First find the volume of the cylinder:

VCYL =

=

=
= 50.2654

Then find the volume of the sphere inside :

VSPH =
=
=
= 33.5103

VCYL = = 50.26

VSPH = = 33.51

Now do the same method for the medium and the large sizes, which will give us:

Medium Sized:

VCYL =

VSPH =

Large Sized:

VCYL =

VSPH =

In conclusion, using the medium size one, one and a half spheres fit in each cylinders :

===

Our assignment for today was Excercise 23, Questions: All. A reminder on Monday, November 24th 2008, is our test on Radicals and Exponents, so study hard.

And our next scribe is caseyh.

Spheres

Check your homework using this online calculator for finding the surface area and volume of a sphere. Just type in the radius and click the [enter] button!

Two Quizzes on Spheres:

Surface Area

Volume

You can also try this bottomless quiz (just keep refreshing the page) for finding the volume and surface area of a sphere. Do as many exercises as you feel you need to until you understand the material well.

I know this was a given homework yesterday but I haven't got time. Now, it's not that I'm doing this for the sake of saying, " I did it! " but because I still want to learn how to evaluate and simplify.

My Muddiest Point!

My muddiest point in pre-cal is:
- word problems with radicals
- converting to radical forms
- writing each radical as a mixed radical

My Muddiest Point

My Muddiest Point:

> In this unit is simplifying or Writing in exponential form with radical Variable's!

> For example this kind of Question?

My Person Muddiest Point

My Muddiest point about Radicals that i am good at:
- Adding radicals
-dividing radical
- evaluating radicals
-and also i can solve any problems of those one, but i am really having trouble with
Word Problems
because i don't really understand that one, and i hope i will understand

MY PERSONAL MUDDIEST POINT.

I pretty much understand most things in this unit but am having trouble with the word problems, I need help understanding what the question is asking and answering it right.

My Muddiest Point

My muddiest points about radicals are:
- word problems
- division of radicals
- evaluating radicals
eg. 4 -1/4

MY muddiest Point.

My muddiest point would be understanding word problems, Cosine and Sine laws, some vocabulary, and not having the notes.

Muddiest point

My Muddiest point in pre-cal is understanding analytical geomerty and slopes, word problems. I am also having trouble with that dividing variables (when ms. ingram was our sub).

Personal Muddiest Point

My most muddiest point is around the time you came back.(not to be mean or anything)
Personally i just got used to how Dr. Eviatar teaches. So yea thats my most muddiest point.
(once again not to be mean or anything)

My Personal Muddiest Point

My personal muddiest point is around the time you came back (not to be mean or anything).
I just got used to how Dr. Eviatar taught, so yeah that is my most muddiest point.(once again not to be mean or anything) ^^

November 20 Pre-Test

Today we had a Pre-Test, these are some the concepts that was included in the Pre-Test.

Rational Numbers

*Can be written as a fraction

*Fractions
*Whole Numbers

*Mixed Numbers

*Decimals that end.

*Decimals With a Pattern.

Irrational Number
*Cannot be written as a Fraction
*Decimals with no end/repeating/pattern.


Radical Operations:
Adding/Subtracting:

When you have the same radicand/ike terms, you just simply add them together.

For Example:





---------------------------------------------------------------------------------------
When both radicands does not have the same value you might consider factoring the number so it can have the same value.

For Example:


------------------------------------------------------------------------------------------
*When a problem has same radicand but does not have the same root, you cannot add them together because they are not like terms.

For Example:



______________________________________________________________

Multiplying:

Dont forget to use FOIL whe multiplying.



---------------------------------------------------------------------------------------
Be careful when subtracting after multiplying! Only add the like terms.
Also don't forget that there's always a one before the root.

____________________________________________________

Rationalizing
The denominator is a sum of 3+√y, so we multiply numerator and denominator by the difference 3 - √y.

------------------------------------------------------------------------------------
The denominator is a difference of √7 - √5, so we multiply numerator and denominator by the sum √7 - √5



The test is on Monday, so be ready for it.

The next Scribe is ARJEL......

Personal Muddiest Point

My muddiest point are:
*Not knowing when to use negative or positive when rationalizing.
*Word Problems (The whole back of the Pre-test!!)
*Help with some of the Vocabulary.

I have to shall call this post "Bob"

My muddiest point(s)? I would have to say:

-working with and index higher than 2

-deciding which pair of a number's factors to use

and

-solving problems like